Shinyoung Yi (이신영, 李神榮)

I am a postdoctoral researcher at the Visual Computing Lab., KAIST, where I earned both my MS and PhD degrees in computer science under the supervision of Prof. Min H. Kim. My research spans computer graphics, vision and computational imaging.

I was previously a research intern at Microsoft Research Asia. I hold a BS in mathematics, physics, and computer science (dual major/minor) from KAIST.

Email  /  GitHub  /  Google Scholar  /  LinkedIn  /  CV

profile photo

Awards

Outstanding PhD Thesis in School of Computing for Year 2024, KAIST, 2025

Stars of Tomorrow Award (award of exellent intern), Microsoft Research Asia, 2023

Top 10 Research Accomplishments, KAIST, 2021 - Differentiable transient rendering

Research

I'm interested in computer graphics and vision. Especially, physically-based rendering and mathematical foundation of computer graphics.

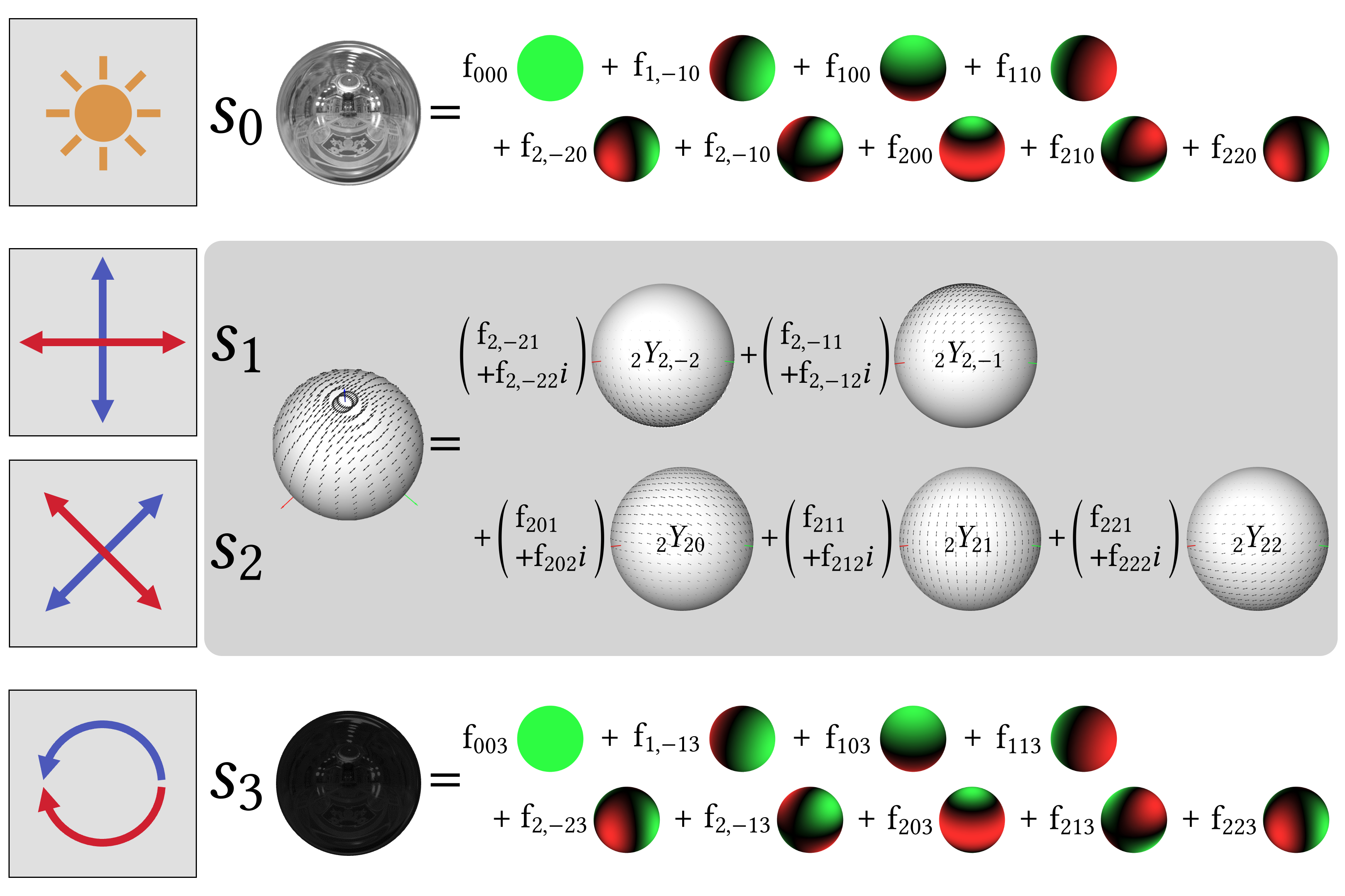
project image

Spin-Weighted Spherical Harmonics for Polarized Light Transport


Shinyoung Yi, Donggun Kim, Jiwoong Na, Xin Tong, Min H. Kim
SIGGRAPH (ACM Trans. Graph.), 2024
code / project page / paper /

A unified theory of spin-0 (scalar) and spin-2 spherical harmonics for a frequency domain analysis of polarized light transport.
project image

Modeling Surround-aware Contrast for HDR Displays


Shinyoung Yi, Daniel S. Jeon, Ana Serrano, Se-Yoon Jeong, Hui-Yong Kim, Diego Gutierrez, Min H. Kim
Computer Graphics Forum (CGF), 2022
code / project page / paper /

An experiment and model for a surround-aware contrast sensitivity. The journal version of a previous work.
project image

Differentiable Transient Rendering


Shinyoung Yi, Donggun Kim, Kiseok Choi, Adrian Jarabo, Diego Gutierrez, Min H. Kim
SIGGRAPH Asia (ACM Trans. Graph.), 2021
code / project page / paper /

The first differentiable transient rendering.
project image

Modeling Surround-aware Contrast Sensitivity


Shinyoung Yi, Daniel S. Jeon, Ana Serrano, Se-Yoon Jeong, Hui-Yong Kim, Diego Gutierrez, Min H. Kim
Eurographics Symposium on Rendering (EGSR), 2021
code / project page / paper /

An experiment and model for a surround-aware contrast sensitivity.
project image

Compact Snapshot Hyperspectral Imaging with Diffracted Rotation


Daniel S. Jeon, Seung-Hwan Baek, Shinyoung Yi, Qiang Fu, Xiong Dun, Wolfgang Heidrich, Min H. Kim
SIGGRAPH (ACM Trans. Graph.), 2019
project page / paper /

A compact single-shot hyperspectral imaging using a diffractive optical element (DoE). The DoE yields a spectrally-varying point spread function which provides a cue for compressive reconstruction.

Educational Materials
project image

Python-based lecture for physics based ray tracing


Educational_material

website /

Developing comprehensive lecture materials on physics-based rendering. These materials are the first Python-based rendering lecture sources utilizing Mitsuba 3, a popular research-oriented rendering system. Compared to existing materials based on heavy C++ implementations, the Python interface significantly enhances accessibility, enabling researchers in fields beyond computer graphics, such as computer vision and remote sensing, to effectively learn rendering concepts

Design and source code from Leonid Keselman's Jekyll fork of Jon Barron's website